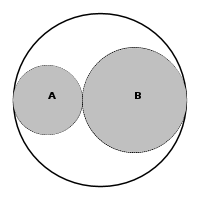
Math Olympiad 5( Week 46 Quiz 9) 2. Two people have two-digit ages. Both age numbers have a digit sum of 11 and an equal digit product. If one person is 9 years older than the other person, how old is the younger person? 3. The distance from place A to place B is 320 miles. Two cars start out from place A to place B at the same time. One car drove at 51 mph; the other car drove at 29 mph. When the faster car got to the place B, it went back immediately. How many hours did it take for them to meet again? 4. There were the equal number of books on two bookshelves. After 49 books were removed from the first shelf, and 119 books were added to the second shelf, the number of books on the second shelf was 8 times as many as on the first shelf. How many books were there on the second bookshelf originally? 5. There are 5 times as much water in the bigger container as in the smaller container. If 5 liters of water are poured out from each of the two containers, there will be 6 times as much water in the bigger container as in the smaller one. How many liters of water did the larger container have at the beginning? 6. A set of 9 coins may contain any combination of pennies, nickels, dimes, or quarters. In how many different ways can the set of coins have a total value of 33 cents? 7. A horse finished 400-yard dash in 40 seconds. What is the speed of the horse in mph? Express your answer as a decimal to the nearest hundredth. Note that 1 mile = 1760 yards. 8. Two circles A and B are enclosed inside a larger circle C. There is no overlap between A and B, and they stretch the entire diameter of the larger circle C. The area of circle C is 100. What is the largest possible non-shaded area inside C? Note that the diagram might not be drawn to scale.
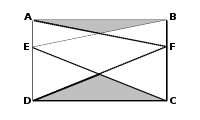
9. ABCD is a rectangle. E, and F are at the same height. If the area of the rectangle ABCD is 30, what is the area sum of the shaded triangles?
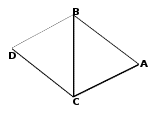
10. Two triangles ABC and BCD share a common side BC. Below are the angles in degrees.
| Angle | ∠BAC | ∠ABC | ∠BCA | ∠CDB | ∠DBC | ∠BCD |
|---|
| Degrees(°) | 66 | 56 | 58 | 54 | 61 | 65 |
|---|
Which of the following is the longest line segment? Note that the diagram might not be drawn to scale.
11. The sides of a triangle are all integer lengths. Two sides have the lengths of 12 and 11. What is the smallest possible perimeter of the triangle? 12. What is the length of EC in the following diagram?
13.
In the figure above, point R lies on segment OP. The area of the circle with center O is 256π, and the length of the line segment OP is 13. What is the area of the circle with center Q? 14.
If the area of the square in the figure above is 100 and the perimeter of each of the 4 triangles is 21, what is the perimeter of the figure (a star) outlined by the solid line? Note that the figure is not drawn to scale. 15. There are two bookshelves A and B. If 392 books were moved from bookshelf A to bookshelf B, the two bookshelves would have the same number of books. If 392 books were moved from bookshelf B to bookshelf A, the number of books on bookshelf A would be 5 times as many as on bookshelf B. How many books are there on bookshelf A? |