Geometry(2)( Week 37 Evaluation) 1. In the figure below, a triangle is inscribed in a circle with one of its side AC through the circle center O. If AB = 8 and BC = 8, what is the area of the circle?
2. What is the maximum area possible if a rectangle has a perimeter of 12? 3.
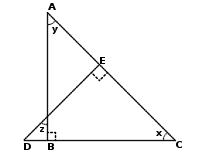
AD bisects both ∠A and the side BC of the ΔABC. Which of the following CANNOT be concluded? Note that the figure is not drawn to scale. 4. ABC and DEC are right triangles. If ∠D = 45° What will be y + z = ? Note that x, y, and z are the degrees of the corresponding marked angles, and the diagram might not be drawn to scale.
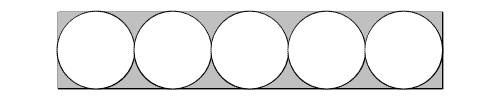
5. A triangle has area of 20 square units and it can fit an incircle with a maximum diameter of 4 unit. What is the perimeter of the triangle in units? 6. The circles and the enclosing rectangle are tangent as shown in the diagram. If the total area of all the circles is 500π, what is the area of the rectangle?
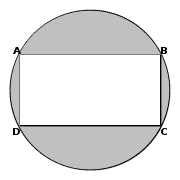
7. Rectangle ABCD is enclosed by a circle with its four vertices A, B, C, D on the circle as shown in the diagram. If AB = 12 and BC = 8, what is the area of shaded shape?
8. ABC is a triangle. If AB is the longest line segment of the triangle, which of the following must be true? Note that the diagram might not be drawn to scale.
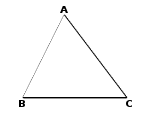
9. ABC is a triangle. If ∠A is the largest angle of the triangle, which of the following could be true? Note that the diagram might not be drawn to scale.

10. In an obtuse triangle ABC with AC = AB, which of the following must be true? |